RESEARCH ON LASSO
SUPPORTING EDUCATORS AND RESEARCHERS
We developed LASSO to support educators and researchers in collecting high quality data using instruments and analyses with strong validity arguments. To support this goal, we investigated two research questions of interest to LASSO-using instructors and researchers:
Are online assessments a good replacement for paper assessments?
What are the best methods for handling missing data?
We also investigated a third research question specifically for researchers

What are the best methods for analyzing large-scale
multi-level datasets?
Nissen et al.2 used a randomized between groups experimental design to investigate whether LASSO administered RBAs provided equivalent data to traditional in-class assessments for both student performance and participation. Analysis of 1,310 students in 3 college physics courses indicated that LASSO-based and in-class assessments provide equivalent participation rates when instructors used four recommended practices (shown in figure 2):(1) In-class reminders, (2) multiple email reminders, and (3) credit for pretest participation, and (4) credit for posttest participation.
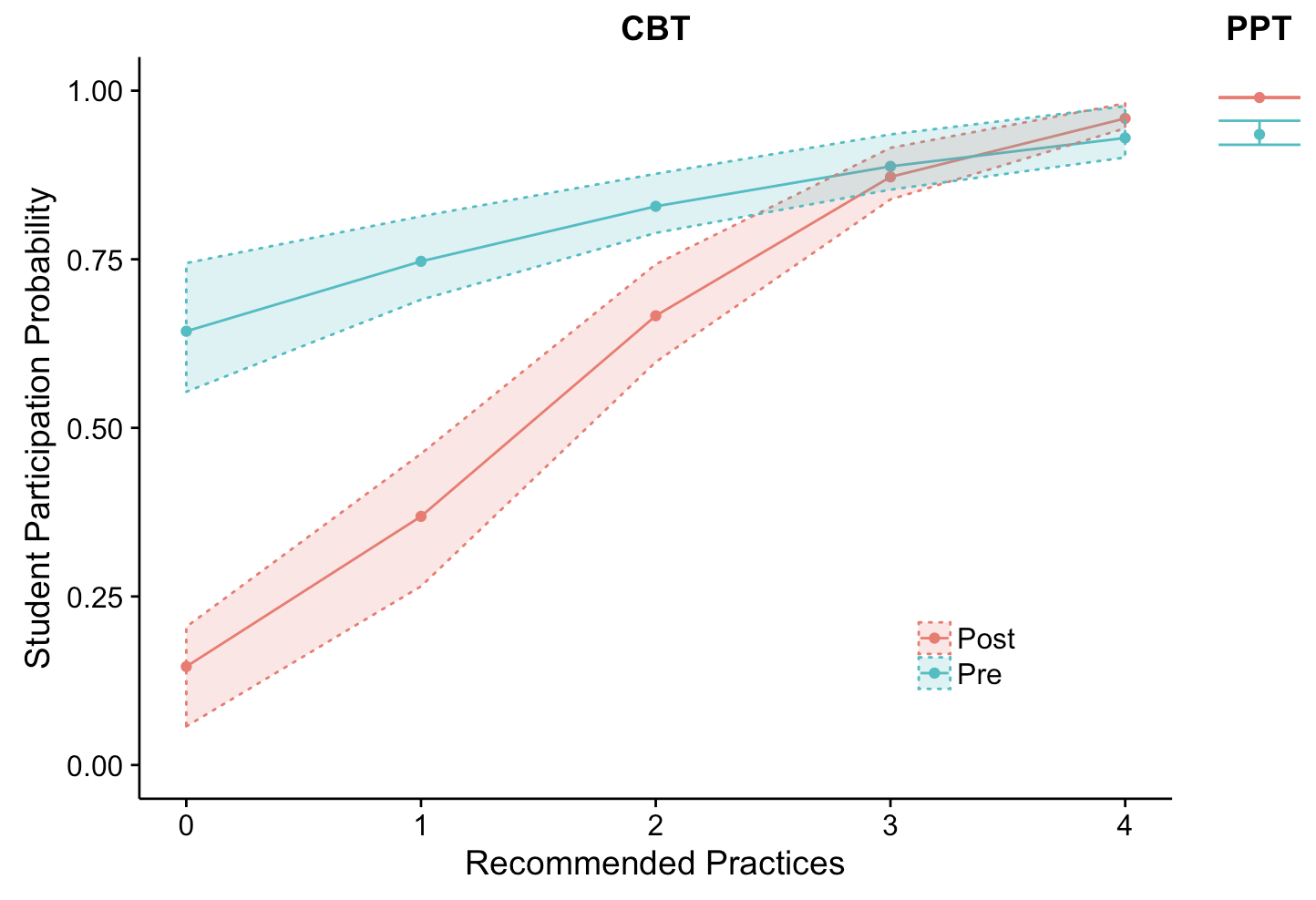
Figure 2. Participation rates on LASSO as instructors increased their use of the recommended practices (e.g., sending email reminders & offering credit) on computer-based tests (CBT) versus paper and pencil tests (PPT). When all 4 recommended practices were used, the participation rates were nearly identical.
Models of student performance indicated that tests administered with LASSO had equivalent scores to those administered in class. This indicates that instructors can compare their data from LASSO to any prior data they may have collected and the broader literature on student gains.
Nissen et al.2 found that students with lower grades participated at lower rates than students with higher grades both in their data. These results indicated a bias toward high performing students for RBAs collected in-class or with LASSO. PER studies most commonly report using complete-case analysis (aka, matched data) in which data is discarded for any student who does not complete both the pre and posttest. Nissen, Donatello, and Van Dusen3 used simulated classroom data to measure the potential bias introduced by complete case analysis and Multiple Imputation. Multiple Imputation uses all of the available data to build statistical models, which allows it to account for patterns in the missing data. Results, shown in Figure 3, indicated that complete-case analysis introduced meaningfully more bias into the results than multiple imputation.
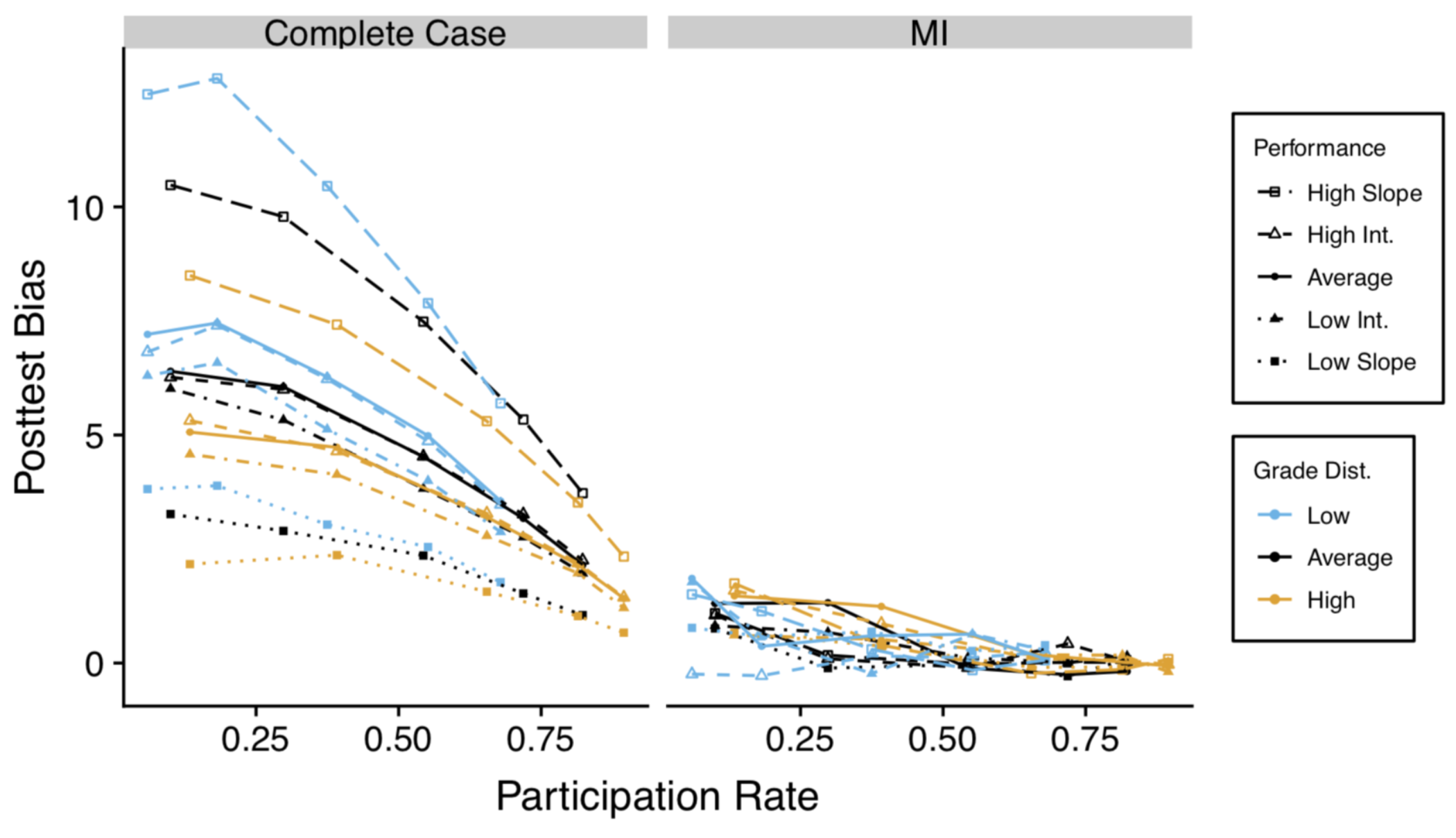
Figure 3. Bias introduced into posttest scores for complete case analysis and multiple imputation.
PER studies often use single-level regression models (e.g., linear and logistic regression) to analyze student outcomes. However, education datasets often have hierarchical structures, such as students nested within courses, that single-level models fail to account for. Multi-level models account for the structure of hierarchical datasets.
To illustrate the importance of performing a multi-level analysis of nested data, Van Dusen and Nissen3 analyzed a dataset with 112 introductory physics courses from the LASSO database using both multiple linear regression and hierarchical linear modeling. They developed models that examined student learning in classrooms that use traditional instruction, collaborative learning with LAs, and collaborative learning without LAs. The two models produced significantly different findings about the impact of courses that used collaborative learning without LAs, shown in Figure 4. This analysis illustrated that the use of multi-level models to analyze nested datasets can impact the findings and implications of studies in PER. They concluded that the DBER community should use multi-level models to analyze datasets with hierarchical structures.
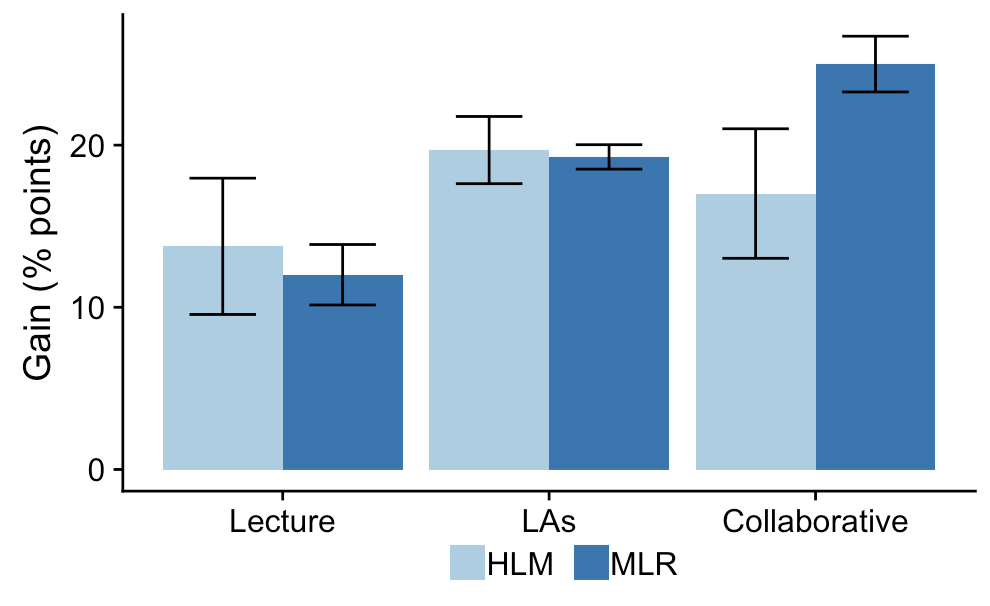
Figure 4. Predicted gains for average students across course contexts as predicted by: a) multiple linear regression and b) hierarchical linear modeling. Error bars are +/- 1 standard error.
References
www.learningassistantalliance.org
Nissen, J. M., Jariwala, M., Close, E. W., & Van Dusen, B. (2018). Participation and performance on paper-and computer-based low-stakes assessments. International Journal of STEM Education, 5(1), 21.
Nissen, J., Donatello, R., & Van Dusen, B. (2019). Missing data and bias in physics education research: A case for using multiple imputation. Physical Review Physics Education Research.
Van Dusen and Nissen (2019). Modernizing PER’s use of regression models: a review of hierarchical linear modeling. Physical Review Physics Education Research.